Recently Spitz (thanks to Software Architect, Clint Weisbrod) implemented new guide lines in Starry Night, graphically linking the Sun and planets (see the fall 2018 Spitz Newsletter and the Copernican Method). This inspired me to consider an animated, user-controllable version depicting Kepler’s Second Law. I have already implemented static images created by Steve Sanders (Eastern University’s Observatory Administrator) for teaching Kepler’s Second Law in Volume 2 of the Spitz Fulldome Curriculum, but static images pale in comparison to animations depicting the same concept.
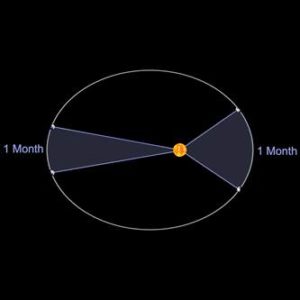
Figure 1 – Kepler’s Second Law from FDC Volume 2
Kepler’s Second Law states that a radius vector connecting a planet to the Sun will sweep out equal areas in equal intervals of time. This paradigm-shattering result enabled the understanding of how planets change velocities in an orderly and systematic fashion (they are actually conserving angular momentum, but that realization would have to wait for Newton). Historic models mimicking the changing speeds of planets were complex and impressive but completely unwieldy when it came to calculations. They were also inaccurate.
What we devised (to be included in Fulldome Curriculum Volume 4) is a new Starry Night feature allowing Kepler’s Second Law to be illustrated for bodies in the solar system (planets, moons around planets, asteroids, comets, etc.), as well as exoplanets around their parent star. The feature allows operators to make a real-time graphical version of the sweeping sections of orbits.
The controls for making Kepler Orbits are shown below:
The operator can enter time intervals for orbital segments (and we included a “Suggest Interval” function, which I almost always use, so beginning users have help in creating the segments). We can show individual orbital areas, and label the results.
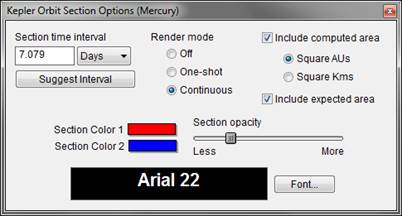
Figure 2 – Kepler Orbit Section option dialog for Mercury
Figure 3a shows the result of running time for Mercury and Figure 3b displays the completed orbit. The numbers in each orbit segment are the numerically integrated areas of the segments, each of which is being calculated for the exact time interval set in the input box of Figure 2.
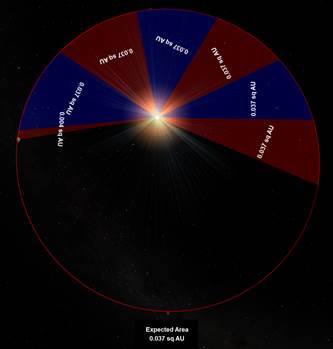
Figure 3a – Mercury beginning to draw Kepler Orbit sections in 7 day intervals

Figure 3b – Mercury completed Kepler Orbit sections in 7 day intervals
Note the Expected Area displayed at the bottom of the figures. This is the analytically calculated area for an orbital segment for Mercury given the time interval specified by the user. You may think, “Of course they are the same.” If you know anything about numerical analysis, it’s quite impressive that the numerical integration techniques implemented in this routine are accurate enough to reproduce the analytical prediction, i.e., validating Kepler’s Second Law.
We are so used to seeing equations predict outcomes that we’ve lost the astonishment of Kepler and Renaissance scientists for the precise nature of the universe, that it could be accurately modeled by mathematical equations!
Let’s take a look at this feature for Halley’s Comet. Because of the extreme eccentricity typical of comets, we’ve only displayed the perihelion passage of this body, as illustrated in Figure 4.

Figure 4 – Perihelion passage of Halley’s Comet in 1986
Figure 5 displays the eccentric (0.56) Venus orbit-crossing asteroid 27 Apollo around the Sun. Venus’ orbit is shown to scale.
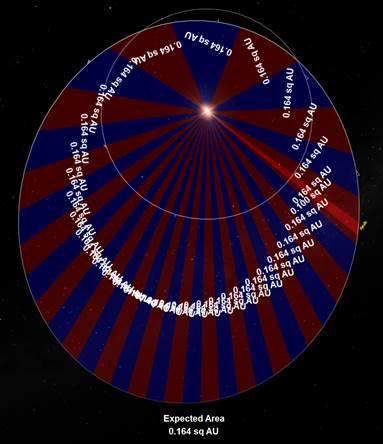
Figure 5 – The orbit of the Venus orbit-crossing asteroid 27 Apollo
Figure 6 displays the very eccentric (0.75) orbit of Nereid, a moon of Neptune. I purposely didn’t display the numerically calculated areas to show what that looks like, i.e., to clean up the display.
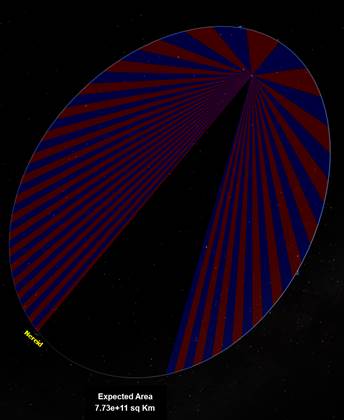
Figure 6 Nereid’s orbit around Neptune, with an eccentricity of 0.75.
As a final example, Figure 7 displays the orbit of the exoplanet HD 87646b. It has an eccentricity of 0.500, an orbital period of 674 days and a semimajor axis of 1.580 AU.
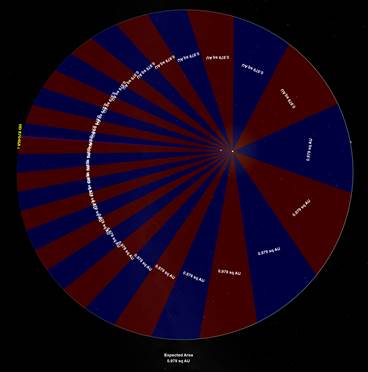
Figure 7 – The orbit of exoplanet HD 87646b.
I sincerely hope that this upcoming new feature in SciDome excites audiences as much as it does all of us who have worked on implementing it! I also am extremely hopeful that when audiences see Kepler’s Second Law in action that they will finally be able to understand more fully what is meant by it.
