Worldwide Reach
Spitz and E&S theaters deliver breathtaking experiences to hundreds of millions around the globe
Countries
Theaters
Years
World Class Clients
Our installations are the focal points of major science museums and planetariums, and deliver signature experiences at the world’s most prominent theme parks and attractions.








Innovation is in our
DNA
1947
First widely used planetarium projector
- Armand Spitz‘s revolutionary Model A1 made the planetarium affordable for schools and museums of all sizes
1963
First graphical computer interface
- Ivan Sutherland invents Sketchpad, considered to be the first computer-aided design (CAD) program – a major breakthrough in the development of computer graphics
1966
Model A3P & “Spitz Classroom”
- The workhorse Spitz A3P went on to become the world’s most popular planetarium projector, with nearly 1,000 installations worldwide
1966
First computer-controlled planetarium
- The Spitz Space Transit Planetarium includes a third axis of rotation and precision planet projector control able to simulate travel away from Earth
1968
First head-mounted VR
- E&S demonstrates virtual reality with a prototype nicknamed Sword of Damocles, in reference to a component suspended somewhat ominously above the operator
1973
First Dome IMAX
- Spitz creates the first dome IMAX theater: a tilted-seating Spitz STS Planetarium which includes a new IMAX dome projector. To this day, IMAX uses Spitz domes exclusively
1977
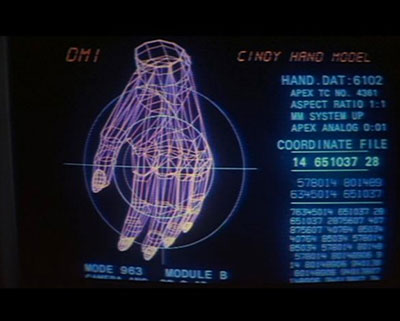
First animated, textured computer model
- The groundbreaking “E&S Hand” also becomes the first 3D computer graphic shown in a Hollywood movie – 1977’s Futureworld
1981
First digital planetarium
- The E&S Digistar offers the first 3D starfields and complex wireframe animations in a planetarium, launching a revolution in immersive visual display
1982
E&S powers Star Trek II SFX
- Digistar provides tactical bridge displays for USS Enterprise, as well as 3D moving starfields which open and close the film
1990
Powder coated dome
- Becoming the standard for IMAX Domes around the world, Spitz electrostatically applies epoxy powder coating to deliver a perfectly uniform optical finish conventional paint can’t achieve
2002
Digistar 3 transforms planetariums
- E&S debuts the first fully interactive real-time 3D planetarium and fulldome 180 x 360 video projection system
2006
Spitz joins the E&S family
- Evans & Sutherland becomes the first full-capability dome theater provider, delivering inner and outer domes, projection and computing, content, theater design, and integration of all elements
2008
First seamless projection dome
- Spitz NanoSeam™ is the first projection dome with no folds, overlaps, or irregularities, making seams invisible under projection. Over 200 have since been delivered
2019
DomeX LED dome
- E&S is leading the revolution in shared immersive experience. DomeX provides brightness and contrast far exceeding conventional projection, heightening the sense that You Are There
2020
Cosm Acquires E&S and Spitz
- E&S and Spitz become cornerstones of Cosm, a global technology company that enables people to experience entertainment in a new way, across three primary markets: Sports and Entertainment, Science and Education, and Parks and Attractions
2020
Cosm Experience Center
- Experience the DomeX LED Dome and our complete technology capabilities at the Cosm Experience Center, our demonstration and R&D facility in Salt Lake City
Immersive Experience is Our Passion
Providing design and engineering, imaging and spatial computing, dome screens and architectural domes, Evans & Sutherland and Spitz are the world’s only turnkey provider of complete dome theaters.