A historical lesson in Volume 2 of the Fulldome Curriculum is the astronomical aspect of the Boston Tea Party. As we learn, Colonists, furious at the tea tax, tossed chests of tea into Boston Harbor on the night of December 16, 1773. Eyewitnesses noted that the chests became stuck in the mud adjacent to the ship and piled up in such a way that the Colonists feared the chests wouldn’t float out to sea and might be partially recoverable. The low tide that night (between 6-9 PM local time), which occurred (coincidentally) simultaneously with the raid, was especially low that night.
Although our lesson concentrates on discovering the Moon’s phase that night, a key element is why both high and low tides were so extreme. It turns out that the Moon was close to New Moon phase and perigee that night, making the tides about as extreme as they ever get. So I’d like to concentrate on explaining why tides occur and why the Moon is the major cause of tides and not the Sun.
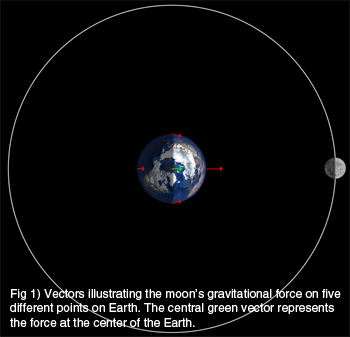 The ancients knew that the Moon caused the tides because the tides roughly coincided with the position of the Moon in the sky. The interval between successive high and low tides is ~13 hours, and the high and low tides occurring the next day were approximately one hour later, mimicking the position of the Moon which moved about 13 degrees to the east each day.
The ancients knew that the Moon caused the tides because the tides roughly coincided with the position of the Moon in the sky. The interval between successive high and low tides is ~13 hours, and the high and low tides occurring the next day were approximately one hour later, mimicking the position of the Moon which moved about 13 degrees to the east each day.
The ancients also noted that the greatest tides occurred during New and Full Moons (spring tides) and the least extreme tides occurred at 1st and 3rd quarter (neap tides). But how the Moon caused the tides had to wait until Isaac Newton. I often ask students: “What causes tides on the Earth?” Their answer is always: “The Moon’s gravity pulling on the water of the Earth.” I then ask them, “Then why doesn’t the Sun cause the tides, since its gravitational pull on the Earth is 180 times stronger than the Moon’s (which is why we orbit the Sun and not the Moon!)?”
 The answer is that it’s the Moon’s differential gravitational force on the Earth that causes the tides. The Earth is close enough to the Moon that the Moon pulls considerably harder on the Earth’s near side compared to its far side. The percentage difference between the Moon’s gravitational pull on the Earth’s near side compared to the far side is 6.9%. The Sun, which is so far away from the Earth that it sees the Earth as essentially a point mass, pulls differently on each side of the Earth by a percentage difference of only 0.017%! Ok, most people (students) will buy this, but do NOT understand why the water bulges on both sides of the Earth.
The answer is that it’s the Moon’s differential gravitational force on the Earth that causes the tides. The Earth is close enough to the Moon that the Moon pulls considerably harder on the Earth’s near side compared to its far side. The percentage difference between the Moon’s gravitational pull on the Earth’s near side compared to the far side is 6.9%. The Sun, which is so far away from the Earth that it sees the Earth as essentially a point mass, pulls differently on each side of the Earth by a percentage difference of only 0.017%! Ok, most people (students) will buy this, but do NOT understand why the water bulges on both sides of the Earth.
Figure 1 illustrates the strength and direction of the Moon’s gravitational pull on the Earth at New Moon, i.e., the Sun and Moon are in the same direction. This was essentially the phase of the Moon during the Tea Party, i.e., a day or so past New Moon (thin waxing Crescent).
 Determining the differential force experienced by the Earth is equivalent to asking, “What does the Earth actually ‘feel’ due to the Moon’s uneven tugging on it?
Determining the differential force experienced by the Earth is equivalent to asking, “What does the Earth actually ‘feel’ due to the Moon’s uneven tugging on it?
We can calculate that by subtracting out the force vector that the Earth experiences at its center from all the other vectors. This is, by definition, the meaning of differential gravitational force.
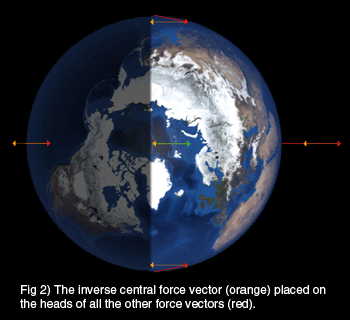
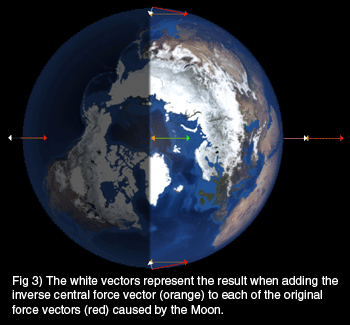
To illustrate this, Figure 2 shows the inverse center vector’s tail (drawn in orange) placed at the head of each force vector. We will add this inverse vector to all five vectors and illustrate their resultants by white vectors in Figure 3.
For clarity, let’s just look at the resultant differential force vectors in Figure 4.
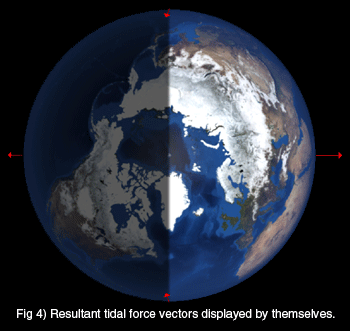 As already noted, there is no vector at the center of the Earth because we added its exact inverse so that it canceled out. (That was the point – asking what does the Earth “feel” is a center of Earth force transformation. Sounds cool anyway…) The remaining vectors make sense if you think about each one of them.
As already noted, there is no vector at the center of the Earth because we added its exact inverse so that it canceled out. (That was the point – asking what does the Earth “feel” is a center of Earth force transformation. Sounds cool anyway…) The remaining vectors make sense if you think about each one of them.
The resultant vector on the right occurs because the Moon pulls hardest on the near side, so subtracting the weaker central force resulted in a vector pointing to the right. The resultant vector on the far side to the left will also make sense because the Moon pulls least on that side, so subtracting the larger central force vector resulted in a force pointing to the left! The resultants on the top and bottom occur because of the slightly different directions that the Moon’s force pulls on those points compared to the direct line at the Earth’s center.
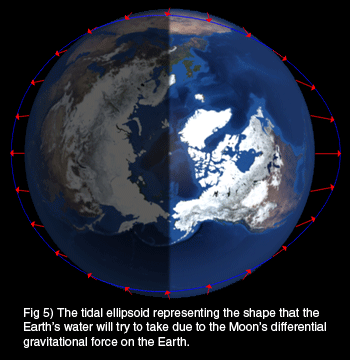
If we continued this exercise at 15-degree intervals (instead of 90-degree intervals) around the surface of the Earth, we would have the resultant vectors shown in Figure 5. The locus of all the vector heads has also been drawn in and this egg shape represents the gravitational equipotential of all the tidal forces, i.e., it’s this shape that the water will attempt to emulate.
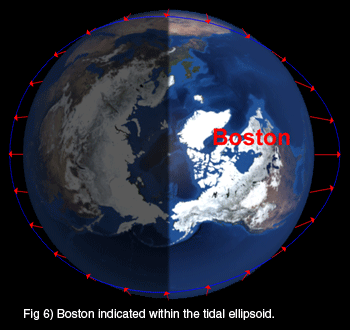
 Ok, now what? Well, let’s label Boston in the diagram and talk about it – see Figure 6.
Ok, now what? Well, let’s label Boston in the diagram and talk about it – see Figure 6.
Remember that the Moon and Sun are off in the direction towards the right in all the figures. What approximate time is it in Boston in Figure 6? With the Sun highest in the sky, it would be noon. (I hesitate to say “directly over your head,” but you know what I mean.) What tide would the folks in Boston be experiencing at this moment?
The highest bulge is in the direction of the Sun and Moon, so they must be experiencing high tide. Now let’s advance 6 hours to sunset, i.e., let’s turn the Earth counterclockwise by 90 degrees, as depicted in Figure 7. (Pretend that the Moon hasn’t moved in those six hours, so that the tidal bulge is still in the same direction.)
This is essentially the situation during the Boston Tea Party! The Sun had set and the thin crescent Moon was setting. Boston was experiencing low tide at this time (as shown in Figure 7) and it was an especially extreme low tide because the Moon was (coincidentally) close to perigee, so its tidal effects were maximized. So, when would Boston experience its next high tide?
 Approximately 6 hours later, near midnight, when Boston was on the opposite side of the Earth relative to the Sun and Moon. Figure 7 implies that the high tide it experiences on the far side is not as high as the one on the near side, and this is exactly the case with the tides! The one facing the Moon is somewhat higher (by a foot or so) than the one on the far side! Most people don’t know this, since diagrams in books always draw the tidal bulge in equal amounts on both sides of the Earth, but (as you can see in our accurately drawn diagrams) they are wrong!
Approximately 6 hours later, near midnight, when Boston was on the opposite side of the Earth relative to the Sun and Moon. Figure 7 implies that the high tide it experiences on the far side is not as high as the one on the near side, and this is exactly the case with the tides! The one facing the Moon is somewhat higher (by a foot or so) than the one on the far side! Most people don’t know this, since diagrams in books always draw the tidal bulge in equal amounts on both sides of the Earth, but (as you can see in our accurately drawn diagrams) they are wrong!
How do you implement this knowledge in the planetarium? If you understand the above analysis, you can understand that indeed the tides will be in synchronization with the position of the Moon relative to your location. So, if you have New Moon, then high tides at your location are going to occur (approximately) at noon and midnight as in our Boston Tea Party example. This is because New Moon is highest and lowest (near your nadir) in your sky near noon and midnight, respectively.
 Actually the tides lag by about an hour because the water is trying to keep up with the Moon and lags behind its position. Let’s not get too technical! We haven’t even worried about the irregular landforms of the continents and how they complicate the actual tide heights, like at the Bay of Fundy!
Actually the tides lag by about an hour because the water is trying to keep up with the Moon and lags behind its position. Let’s not get too technical! We haven’t even worried about the irregular landforms of the continents and how they complicate the actual tide heights, like at the Bay of Fundy!
What about the tides at Full Moon? Full Moon will behave similarly to New Moon, i.e., high tides will occur when Full Moon is (approximately) highest and lowest in the sky, i.e., midnight and noon.
What about 1st quarter? Again, the principle is exactly the same! When 1st quarter is highest and lowest in the sky, you should be experiencing high tides. 1st quarter is highest at approximately sunset and lowest (near your nadir) at sunrise. Likewise, 3rd quarter is highest and lowest at sunrise and sunset (respectively).
Confused? It’s ok. What you need to do is understand that the tidal bulge (high tide) is always trying to point to the Moon. So high tide will follow the Moon and the Earth “rotates” within the tidal bulging water so to speak. If you carefully work through the explanation and figures above, you should be able to comprehend when to expect high and low tides! If you can convey this to your audiences, they will have re-discovered what the ancients knew and why knowing the position of the Moon in the sky was important to them!
