
Jan 17, 2017 | History, Orbits, SciDome Tips, Time

Benjamin Franklin
Today is Benjamin Franklin‘s birthday under the calendar we use today, although he was born on the 6th of January of 1706. He was born before the Gregorian calendar reform was implemented in the English-speaking world.
The Gregorian calendar reform adjusted the way that leap years are counted. Instead of observing an intercalary day in February once every four years, the Gregorian observes one such day every four years except when the year is divisible by 100, except when the year is also divisible by 400.
The exact time it takes the Earth to go around the Sun 365.2422 days, not an integer number of days. During the Julian period the remainder was reduced from the 365-day year by adding a leap day every four years. However, the remaining error compounded. The Gregorian calendar uses 97 leap days every 400 years instead of 100 leap days, so the average length of the Gregorian year is 365.2425 days. The Gregorian change also ran a correction to delete the accumulated lag, which had grown to 10 or 11 days.
The new calendar came into force in Roman Catholic states in 1582.
Denmark switched to the Gregorian calendar in mid-February 1700.
The British Empire made the change in 1752.
For any celebrity birthdates you want to celebrate that are older than a certain limit and come from a certain country, it may be important to see if they should be read out as a Julian or a Gregorian date.
If you bring up Starry Night with a date of October 4th, 1582, and advance by one day, you can observe the 10-day correction when the Gregorian calendar was assumed.
The only alternative to observing the ten-day gap that followed in 1582 when looking at earlier dates is to use the proleptic Gregorian calendar, which eliminates the need for a Julian calendar correction when observing past dates. I wouldn’t recommend using the proleptic Gregorian calendar for earlier dates because the people of the time did not use it either, and Starry Night will read out those dates using the Julian.
By 1752, when the British Empire adopted the Gregorian, the accumulated error had grown to 11 days, and the change was reflected in the British colonies that later became the United States. Benjamin Franklin had already been publishing Poor Richard’s Almanac since 1733, and he included a long explanation of the calendar reform in the 1752 edition.
(When Abraham Lincoln used an almanac to show the phase of the moon during the Trial by Moonlight in 1858, as in our Fulldome Curriculum, he was taking a page from one of the most popular kinds of document in the English language other than the Bible.)
The calendar reform of 1752 didn’t catch everyone by surprise, and although the correction was run in September 1752, Franklin had adequate notice before his publication deadline the previous year. The British Parliament passed the new rule as the Calendar (New Style) Act 1750, although the code used for that legislation was “24 Geo. 2 c.XXIII”, meaning it was the 23rd piece of legislation that received royal assent in the 24th year of the reign of King George II. King George had commenced his reign in 1727.
The first point of the new law, before the Julian correction, was to correct the date of the beginning of the legal new year. Although different cultures have strong traditions to begin the new year on January 1st, even now it is impractical for all of our traditions to line up on a single start date: the school year and the NFL season being a couple of examples. The British Empire up to 1752 had observed the start of its legal year on March 25th. The law passed in 1751 corrected the New Year to January 1st at the beginning of 1752, so the official year 1751 was only 282 days long.
Starry Night does not incorporate any of the other weirdness around calendar reform, except that the new year always starts on January 1st, and there is a year Zero in between the BC and CE periods. (ATM-4 does not calculate a Year Zero).
Happy Birthday to Ben Franklin, who was not born on Blue Monday (It was a Sunday in both calendars, and the days of the week have never accumulated an error).
Sep 21, 2015 | Constellations, Time
The pointer stars Merak and Dubhe point at Polaris and go once around per sidereal day, every 23 hours 56 minutes and 4 seconds. By making a daily correction it is possible to estimate the time at night using these three stars.
One point on this is pretty much intuitive. What is the Right Ascension of Merak? Well, it’s about the same as Dubhe, because a straight line joins both stars to the axis of the celestial clock, the north celestial pole.
But what is that angle, really? Well, it’s 11 hours of Right Ascension. Or, if you use Daylight Saving Time, it appears to be 12 hours.
Thanks to “reasons”, we now spend at least 7 months of the year on Daylight Saving Time, and this helps to make the Big Dipper Star Clock easier to use. At midnight Eastern Daylight Time on September 21st (most years, September 22nd this year), the Autumnal Equinox, the line between Polaris, Merak and Dubhe points straight down to the northern horizon. At midnight Eastern Daylight Time on March 21st, the Vernal Equinox, the line between Polaris, Merak and Dubhe points straight up to the zenith.
On another day of the year, at the moment when the line joining Merak, Dubhe and Polaris is vertical in either direction, if you know the date, you can make an estimate of the time in Daylight Saving Time.
- Count the number of days before or since September 21 or March 21
- For each day before September 21st, imagine winding your mental clock forward from midnight by 4 minutes. If after September 21st, imagine winding your clock back 4 minutes per day. If your index date is March 21st, use the same directions.
So because tonight is 0 days after September 21st, at the moment tonight when the line between Polaris, Merak and Dubhe points straight down to the northern horizon, you can estimate that it’s about 0*4 minutes before midnight, Eastern Daylight Time. (copy and paste, and replace the zeroes for different dates.)
This system doesn’t work perfectly because it’s the same Daylight Saving Time in Detroit as it is in Boston, although the angles of objects in the sky are different. But it is predictable, if you know that you live east or west of the Central Meridian of your Time Zone, to expect objects in the sky to run reliably fast or slow.
Please refer to the Bradstreet Fulldome Curriculum Vol. 2 Minilesson ‘Time Zones’ and the printed lesson plan in the binder for more detail on time zones. The asterism line representing the Pointer Stars, and the Meridian to show the time when the Pointer Stars are vertical, can be drawn in with Starry Night, and in ATM-4 as well. Please refer to the FDC 2 ‘Hour Angles’ Minilesson and its printed lesson plan to interpret how to use other objects in the sky as a star clock.
Because the Pointer Stars are vertical at (DST) midnight on the Equinoxes, they are terrifically useful for this, but the Minilesson might suggest stars for you that have hour angles that are also convenient to remember for relating to the dates that index our seasons. Right-click on a star and select ‘Hour Angle Lines’ to get a dynamic readout of the time since the last moment it crossed the local meridian to the south. The minilessons ‘Time LAST (Local Apparent Solar Time)’ and ‘Time LMST (Local Mean Solar Time)’ use very similar tools.
Apr 20, 2015 | Fulldome Curriculum, Planets & Moons, Scientific Method, Solar System, Time
In the 17th century the speed of light was unknown, and scientists questioned whether it had a finite value. Descartes argued that if the speed of light was finite, when we looked out into space with telescopes we’d be looking into the past. That idea was so off-putting, he concluded the speed of light must be infinite.
We now know it’s not infinite. If it were, the universe couldn’t exist. Remember Einstein’s famous E=mc²: if the speed of light c was infinite, the amount of energy contained in any amount of matter would be infinite! Good luck with that…
Ole Roemer, a Danish astronomer in the 17th century, stumbled upon the speed of light during timing observations of the emergence of Jupiter’s closest Galilean moon, Io, from behind the planet’s limb. He noticed the moon’s appearances didn’t match his predicted times, and by studying them through the year realized it was ahead or behind the predicted time, depending upon how far away Jupiter was from Earth! He correctly reasoned that this variation was not due to some strange inconsistency with Io’s orbit but rather that he was observing what is now called the light-time effect.
Starry Night simulates the light time effect, so we can reproduce Roemer’s 1676 measurements of Io’s emergence from Jupiter’s limb to directly show the light time effect, and even measure the speed of light.

Figure 1: Io emerging from Jupiter’s eastern limb
Figure 1 shows Io emerging from Jupiter’s eastern limb. This view was measured by Roemer in Copenhagen on November 9, 1676. Using Starry Night’s ability to transport us anywhere in space, we can specify a direct route to Jupiter but hold the time constant.
In other words, if we could transport instantly to 0.20 AU from Jupiter (an arbitrarily distance for a nice view of the scene), what would we see? As we travel to Jupiter, we’ll see Io appear to move further and further eastward from the limb even though time has stopped and we’re traveling on a direct line to Jupiter, as shown in Figure 2.

Figure 2: Io appears farther from Jupiter as we reduce our distance
If the speed of light were infinite, when we transported to Jupiter Io would be emerging from the limb, the same view as from Copenhagen. Because the light time effect is built into Starry Night, we see Io has actually emerged significantly past the limb. In other words, on Earth we saw Io just emerging from Jupiter’s limb, but in the neighborhood of Jupiter it has already long since passed from behind the limb!
The difference occurs because of the light time effect.
We can measure the speed of light directly from these observations. We know the distance we covered in our journey from Earth (5.326 AU = 7.968 x 108 km). We can now step back time and return Io back to its emerging position from Jupiter’s limb as seen from this nearby location to Jupiter. If we place Io back on Jupiter’s eastern limb by reversing time in Starry Night, it takes 44m 20s to do so, or 2660 seconds. To estimate the speed of light, we simply take the distance we traveled and divide it by the time, as follows:

Thus we obtain a value for the speed of light only 0.08% different from the actual value of 299,792 km/s!

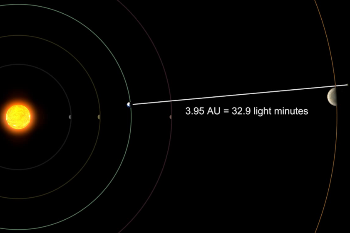
Figure 3: Line of sight from Earth to Jupiter’s limb
Steve Sanders (Eastern University Observatory Administrator) and I have created a simulation which clearly illustrates this phenomenon, as seen in the figures below. This simulation will be included in the release of Volume 3 of the Fulldome Curriculum and you can preview it on Youtube.
Figure 3 shows the line of sight from Earth to Io as it has emerged past Jupiter’s limb, the event that Roemer was measuring. We depict the event close to opposition with Jupiter (Earth’s closest approach to the planet) and the distance between the bodies is approximately 3.95 AU = 3.67 x 108 million miles.
The same event is shown in Figure 4 when Earth and Jupiter are nearing conjunction (Jupiter nearing a syzygy with the Earth and Sun in between). Note that the distance separating the planets is now 5.75 AU = 5.34 x 108 million miles.

Figure 4: Earth and Jupiter nearing conjunction
Roemer measured the emergence of Io as being about 15 minutes later than when this emergence occurred close to opposition and attributed the lateness (correctly) to the extra distance that the light had to travel across the Earth’s orbit.
If you assume that this tardiness is entirely due to the extra time required for light to travel the extra distance, you can estimate the speed of light as follows:

The value of the astronomical unit at that time was very crudely known, so Roemer’s value for the speed of light was not nearly this accurate, but nonetheless he demonstrated that the speed of light was finite, and its value was of this order.
We encourage SciDome operators to use the Roemer Speed of Light minilesson in Volume 1 of the Fulldome Curriculum, along with our new simulation. The discovery of the finite speed of light forever changed our view of the universe, turning our distance-shrinking telescopes into literal time machines as we explore back into our cosmic past.
Feb 28, 2012 | Fulldome Curriculum, Time
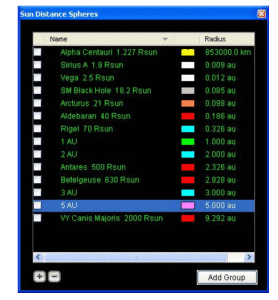
Figure 1: Stars added to Sun Distance Spheres
Distance Spheres included in Starry Night allow “Cosmic Zoom” sequences in our domes. However, I also use them to show audiences scale sizes of stars, the Milky Way’s supermassive black hole, and the speed of light.
In a previous article I described the upcoming “Stellar Sizes” minilesson from the Fulldome Curriculum Volume 2. This program compares the sizes of a dozen different stars to each other on the dome. Here’s another captivating way to illustrate stellar scales, but this time compared to the size of the Solar System on the dome making use of Distance Spheres in Starry Night Dome.
I’ve added new Distance Spheres centered on the Sun and made them the appropriate scale according to the sizes of the stars as given in Starry Night and the scientific literature. The stars added as Distance Spheres are shown in Figure 1.

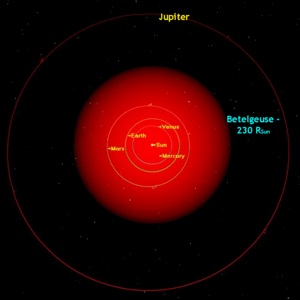
Figure 2: Betelgeuse compared to the Solar System
We can easily add a star’s size to its label name, so as they appear in the dome, their sizes will also show. I’ve colored them appropriately either by temperature or my prejudiced preference. It’s possible to change their opacities so that they look gaseous but you can also see planetary orbits through them, as shown in Figures 2 and 3 which show Betelgeuse and VY Canis Majoris (arguably the largest star known in the Milky Way).
I’ve also added the supermassive black hole that lurks at the center of the Milky Way, which is almost the same size as the star Arcturus. It’s very interesting to see how “small” this 4.3 million solar mass object is compared to the Solar System, as shown in Figure 4.

VY Canis Majoris compared to the Solar System
You can turn various spheres on and off in the dome via SciDome’s “QuickSphere” cue (QS) and or by loading various Starry Night files.
Another useful trick is hidden in a special Distance Sphere which is centered on the Earth, namely the time-varying Radio Sphere. The size of this sphere depends on the date you look at it as it’s expanding at the speed of light. The beginning point in time for this sphere is 12/12/1901 at 14:29:59 UT. So, I’ve set up a Starry Night simulation far enough away from the Earth to see the Moon’s orbit easily with the time stopped.
I tell my audience to watch carefully and they will see the light sphere expand away from the Earth in real time and reach the Moon’s orbit in 1.3 seconds, as seen in Figure 5.
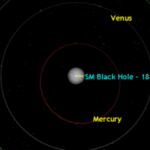
Figure 4: Supermassive Black Hole of the Milky Way compared to the Solar System
You can also increase your elevation to encompass larger volumes of space to watch this sphere expand into the solar system. It’s educational to emphasize that, although light makes it to the Moon in slightly more than one second, it takes minutes to reach the planets, etc.!
I’ve found these to be great tricks for showing students the size of stars and our supermasive black hole compared to the size of our Solar System as well as illustrating the speed of light. I highly recommend that you play with this wonderful new tool in our SciDome teaching arsenal!
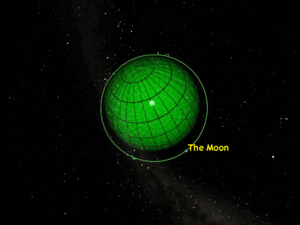
Figure 5: Light Sphere after traveling one second, almost to the Moon’s orbit













